YTM- yield to maturity is defined as that discount rate (“k d ”) at which the present value of future cash flows from a Bond equals its Market Price.
Further YTM is used for bonds or debentures. Therefore, YTM is relevant for valuation of debt funds.
1.What is YTM-Yield to maturity?
YTM-Yield to maturity is annual expected return of a bond if held until maturity. Further, yield to maturity provides investor with an accurate idea of the value of bonds coupon payments. And value of maturity by accounting for the time value of money.
YTM- yield to maturity is defined as that discount rate (“k d ”) at which the present value of future cash flows from a Bond equals its Market Price.
YTM provides annual return that is expected from bond if investors hold till maturity.
Further, coupon payment is the annual interest rate that must be paid to bondholders. And it is fixed rate.
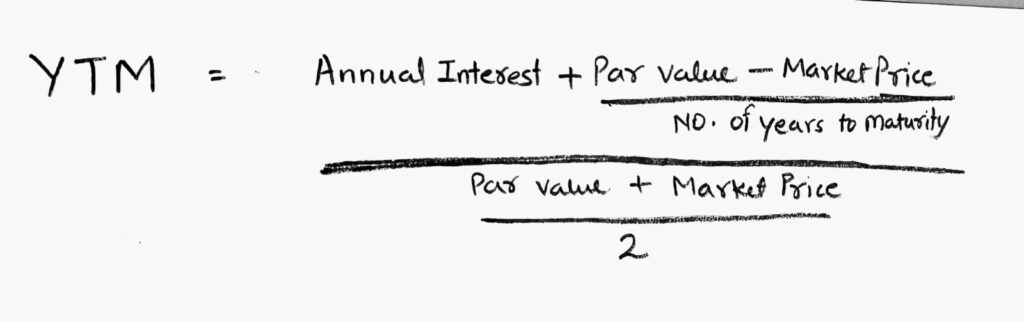
Formula for YTM- Yield to maturity
The formula for YTM is as follows:
Some Basics of YTM
- Par Value: Value stated on the face of the bond of maturity.
- Coupon Rate: A bond carries a specific interest rate known as the Coupon Rate. The coupon can be paid monthly, quarterly, half-yearly or annually.
- Maturity Period: Total time till maturity.
- Redemption : Bullet i.e. one shot repayment of principal at par or premium.
Price Yield Relationship
A basic property of a bond is that its price varies inversely with yield. The reason is – as the
required yield increases, the present value of the cash flow decreases; hence the price decreases and vice versa.
Relationship Between Bond Price and Time
- Since the price of a bond must equal its par value at maturity (assuming that there is no risk of default), bond prices change with time and they approach to the par value of the bond.
- Further, it means that if a bond is trading at premium, its price will decrease over time and if a bond is trading at a discount, its price will increase over time.
Duration of bonds
Duration is the weighted average time within which an investor gets back the promised principal and the promised YTM.
Investment coupon bearing bond always has a duration which is lesser than its maturity. Further, higher the coupon rate, lesser would be the duration and higher the yield -to-maturity , lower will be the duration of bond.
It measures how quickly a bond will repay its true cost . The longer the time it takes the greater exposure the bond has to changes in the interest rate environment and hence , higher interest rate risk.
In addition, duration is also a measure of interest rate risk – higher duration implies higher interest rate risk and lower duration means lower interest rate risk.
Following are some of factors that affect bond’s duration:
i) Time to maturity: The shorter-maturity bond would have a lower duration and less interest
rate risk and vice versa.
ii) Coupon rate: Coupon payment is a key factor in calculation of duration of bonds. The higher the coupon, the lower is the duration and vice versa.
iii) Yield-to-maturity: Higher yield-to-maturity means lower duration and hence, lower
interest rate risk and vice versa.
Although there are many formulae to calculate the duration. However, following are commonly used methods:
a) Macaulay Duration:
This formula measures the number of years required to recover the true cost of a bond, considering the present value of all coupon and principal payments received in the future.
The formula for Macaulay duration is as follows:

Where,
n = Time to maturity
C = Cash flows (Coupon Amount)
i = Required yield
M = Maturity (par) value
P = Bond price
b) Modified Duration:
This is a modified version of Macaulay duration which takes into account the interest rate changes because the changes in interest rates affect duration as the yield gets affected each time the interest rate varies.

Where,
n = Number of compounding periods per year
YTM = Yield to Maturity
Example
Nominal value of 10% bonds issued by a company is 100. The bonds are redeemable at 110 at the end of year 5. Determine the value of the bond if required yield is (i) 5.1%, (ii) 10%
Case (i) Required yield rate = 5.1%
| Year | Cash Flow (₹) | DF 5.1% | Present Value (₹) |
| 1-5 | 10 | 4.3175 | 43.175 |
| 5 | 110 | 0.7798 | 85.778 |
| Value of bond | 128.953 |
Case (ii) Required yield rate = 10%
| Year | Cash Flow (₹) | DF 10% | Present Value (₹) |
| 1-5 | 10 | 3.7908 | 37.908 |
| 5 | 110 | 0.6209 | 68.299 |
| Value of bond | 106.207 |



